ERJ Brainteaser: August

Question 5: Small wonder

What is the smallest number, besides 1, that is one less than twice its digits reversed?

Answer: The answer is 37, as neatly worked out (see Solutions below) by: Stephan Paischer, head of product management special products, Semperit AG Holding, Vienna, Austria; Michele Girardi, quality manager, Scame Mastaf SpA, Suisio, Italy; and Sudi Sudarshan, strategic market & technology insights lead, Bridgestone Americas Inc., USA. Special mention also to Andrew Knox, Rubbond International, Ohé en Laak, The Netherlands; and Peter D. Talbot, research scientist, Chem-Trend LP, Michigan, USA, whose interpretations of the teaser led to answers ‘the square root of 1’ and ‘minus 1’ respectively. 

Solutions

Stephan Paischer

(37 x 2) – 1 = 73

I found it by trying as follows:

For the smaller number (with reversed digits), the second digit needs to be more than double the first one.

So only the following apply: 13, 25, 37, 49

And from all of these, only 37 fulfils the condition given.

Sudi Sudarshan

My answer is 73.

Solution: Two ways I solved this –

(1) by trial and error

73 = 2*37 – 1

(2) algebra-aided trial and error

No other one-digit number meets the criterion.

If ab is a two-digit number that meets the criterion.

Value of ab = 10a+b

Value of ba = 10b+a

ab has same value as  2(ba) – 1

10a+b = 2*(10b+a) – 1 = 20b + 2a -1

8a = 19b – 1

Since 8a is even, 19b – 1 is even or 19b is odd or b is odd.

If b = 1, 19b-1 = 18, which is not a multiple of 8

If b = 3, 19b-1 = 19*3-1 = 56 = 8*7

So, a=7, b=3 and the number is 73.

Michele Girardi

Hello everybody, the answer is 73 .

There's no solution in the numbers between 2 and 9, let's try the 2 digits numbers .

Calling x the number and a,b its digits , it's

x = a+10b

x = 2*(b+10a)-1

a+10b = 2b +20a -1

b = 1/8*(19a-1)

since it's b <= 9 it's

1/8*(19a-1)<=9

19a-1 <= 72

a <= 73/19 = 3.8

trying a from 0 to 3 until  b is integer, there's only the solution  : a=3,  so  b=7  and x=73

Question 4: Next number 

65536256, 25616, 164, ?

Answer: This week’s teaser sparked some fine replies: from an “insane allegation” that there was a mistake in the question – as if that could ever happen! – to a ‘triple go’, and a reworking of an old Frank Sinatra hit (see Solutions below). Very nicely done to: John Coleman , membership manager, Circol ELT, Dublin, Ireland; David Mann, key account manager, SPC Rubber Compounding, UK; Michele Girardi, quality manager, Scame Mastaf SpA, Suisio, Italy; Andrew Knox, Rubbond International, Ohé en Laak, The Netherlands; Hans-Bernd Lüchtefeld, marketing manager – business vertical mobility, segment fibers, Indorama Ventures, Germany; Frank Bloemendaal, manager R&D, Polycomp, Vorden, The Netherlands; Joe Suter, Endurica LLC, USA; Sudi Sudarshan, strategic market & technology insights lead, Bridgestone Americas Inc., USA; and everyone else who had a go.

Solutions

John Coleman

Where n = 256:

65536256 – concatenate(n^2,n)

25616 - concatenate(n,sqrt(n))

164 - concatenate(sqrt(n),sqrt(sqrt(n)))

Therefore, 42 - concatenate(sqrt(sqrt(n)),sqrt(sqrt(sqrt(n))))

David Mann

Disguised squares?

42

Michele Girardi

Hello everybody,

The answer is 42.

The series can be rewritten  as couples

(65636;256), (256;16), (16;4) or

(2^16;2^8), (2^8;2^4),(2^4;2^2)

the next one is (2^2;2^1) , in the original notation 42. Cheers.

Andrew Knox

By splitting the numbers into digits to the left and to the right as highlighted above, the number to left can be formed by squaring each part and setting the products next to each other to form the next number to the left.

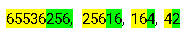
Pretty bizarre, but the next number to the left would then be 429496729665536 (had to turn my phone on it's side to get the whole number). There is no integer that would continue the sequence to the right, but if there were, it would begin with a 2.

Sudi Sudarshan

My answer is 42

The first number, 65536256, is the concatenation of 65536 and its square root 256.

The second number, 25616, is the concatenation of 256 and its square root 16

The third number, 164, is the concatenation of 16 and its square root 4

The fourth number is the concatenation of 4 and its square root 2, hence 42

Joe Suter

In three consecutive emails: 4 is the next number (4x4=16, 16x16=256, 256x256=655362) ... Oh wait It’s 2!... Sorry 42.

Hans-Bernd Lüchtefeld

My way:

And now, the result is near

And so I face the final click

My friend, I'll say it clear

I'll state my calculation, of which I'm certain

I did it my way ... ?

Split the number and then calculate the square root to get the next number:

65536|256 > sqrt 65536 & sqrt 256 > 256 & 16 > 25616

256|16 > sqrt 256 & sqrt 16 > 16 & 4 > 164

16|4 > sqrt 16 & sqrt 4 > 4 & 24 > 42!

Question 3: Connected cities

What do these cities have in common?

Pretoria, Rome, Valletta, Washington, Wellington.

Answer: As well as being capitals, these cities are named after people: Washington: after first US president, George Washington; Valletta, after Jean Parisot de Valette, who defended Malta from invasion; Rome, after the Italian capital’s founder Romulus; Wellington, the New Zealand capital, after English military leader the Duke of Wellington; and South Africa's Pretoria after pioneer Marthinus Pretorius.

Very well done to: David Mann, key account manager, SPC Rubber Compounding, UK; John Bowen, consultant, Bromsgrove, UK;  Michele Girardi, quality manager, Scame Mastaf SpA, Suisio, Italy; Andrew Knox, Rubbond International, Ohé en Laak, The Netherlands; Sudi Sudarshan, strategic market & technology insights lead, Bridgestone Americas Inc., USA; and everyone else who had a go.

Question 2: Number nine

20 = 12, 6 = 3, 3 = 6, ? = 9

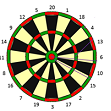Answer: Okay, not so easy after all: it took a couple of days and a couple of clues before a select group of readers recognised this as a sequence of scores on a dartboard based on clockface position: 20=12, 6=3, 3=6 and11=9. Very well done to: Peter D. Talbot, research scientist, Chem-Trend LP, USA; Andrew Knox, Rubbond International, Ohé en Laak, The Netherlands; John Bowen, consultant, Bromsgrove, UK; Michele Girardi, quality manager, Scame Mastaf SpA, Suisio, Italy; Jose Padron, laboratory analyst, Toyoda Gosei, Waterville, QC, Canada (many thanks for the image); Sudi Sudarshan, strategic market & technology insights lead, Bridgestone Americas Inc., USA; and everyone else who had a go.

Question 1: You cannot be series!! 

After a bad-tempered tennis match, John is too agitated to remember the third, two-digit number of the security code on his changing-room locker. Can you help calm him down?

11,23, _, 41

Answer: Key to this very tricky teaser was to recognise this as a sequence of two-digit ‘additive primes’. So, note that the first number 11 (eleven), for example, is a prime number. Then, as the two digits added together equal another prime number 2, this is an ‘additive prime’. From this logic, the sequence on the lock is 11, 23, 29, 41. See  Solutions (with some alternative approaches) below: no wonder our tennis star was so frazzled!

Extremely well done to: David Mann, key account manager, SPC Rubber Compounding, UK; Sudi Sudarshan, strategic market & technology insights lead, Bridgestone Americas Inc., USA; Michele Girardi, Scame Mastaf Spa, Suisio, Italy; Hans-Bernd Lüchtefeld, marketing manager – business vertical mobility, segment fibers, Indorama Ventures, Germany; and everyone else who had a go.

SOLUTIONS

David Mann

Using a Wiki Fandom definition that an additive prime is a prime number where the sum of its digits is also prime, the missing one would be 29.

Sudi Sudarshan

I believe these are Sophie Germain (SG) primes, where each member of the group is a prime number p for which 2p+1 is also a prime.

2              2*2+1 = 5 prime SG

3              3*2+1 = 7 prime SG

5              5*2+1 = 11 prime SG

7              7*2+1 = 15 not prime

11           11*2+1 = 23 prime SG

13           13*2+1 = 27 not prime

17           17*2+1 = 35 not prime

19           19*2+1 = 39 not prime

23           23*2+1 = 47 prime

29           29*2+1 = 59 prime

31           31*2+1 = 63 not prime

37           37*2+1 = 75 not prime

41           41*2+1 = 83 prime

So members of this group that are also two-digit numbers are 11, 23, 29, 41...  So the missing number is  29

Michele Girardi

The complete series may be 11,23, 29, 41, which belongs to the  "Sophie Germain" primes

2, 3, 5,11,23, 29,41, 53, 83

Hans-Bernd Lüchtefeld

A prime number p is a Sophie Germain prime (SGP) if 2p + 1 is also prime. The number 2p + 1 associated with a Sophie Germain prime is called a safe prime. For example, 11 is a Sophie Germain prime and 2 × 11 + 1 = 23 is its associated safe prime. The primes are named after French mathematician Sophie Germain (1 April 1776 – 27 June 1831).

The first SGP < 1.000 are: 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359, 419, 431, 443, 491, 509, 593, 641, 653, 659, 683, 719, 743, 761, 809, 911, 953